Il teorema di Gauss rappresenta lo strumento più utile per calcolare il campo elettrico generato da distribuzioni di carica. Le sue formule dipendono dalla simmetria della distribuzione di carica e dalle caratteristiche geometriche del sistema.
I corsi ADT ti offrono:
- materiale di studio completo 📖
- lezioni live e on demand con docenti qualificati ed esperti nella preparazione al TOLC 🧠
- simulazioni illimitate con oltre 36.000 quiz ministeriali e tantissime modalità di esercitazione sulla nostra piattaforma Futura 💯
- gruppi classe dedicati per interagire con gli altri studenti che si stanno preparando con te 📱
- chat diretta con il tuo tutor personale per ottenere supporto anche dopo l’orario di lezione 📚
Nei prossimi scroll ripassiamo il funzionamento del campo elettrico e vediamo le formule per calcolarlo con semplicità e precisione con il teorema di Gauss 📱
Calcolo del campo elettrico
Il campo elettrico può essere calcolato in diversi modi, a seconda della distribuzione delle cariche e della simmetria del problema. Un metodo comune è usare la legge di Coulomb per cariche puntiformi o la legge di Gauss per problemi con una simmetria ben definita (come la simmetria sferica, cilindrica o planare).
Vediamo questi due metodi:
- La legge di Coulomb descrive il campo elettrico creato da una carica puntiforme. Il campo elettrico E generato da una carica puntiforme ( Q ) a una distanza ( r ) dalla carica è dato da:
E = 1/4πεo*Q/r2*r
dove:- εo è la costante dielettrica del vuoto ⚡️
- r2 è la distanza dal punto dove si misura il campo alla carica 📏
- r è il vettore unitario che punta dalla carica al punto di misurazione ✍️
- La legge di Gauss permette di calcolare il campo elettrico quando la distribuzione di carica ha una simmetria regolare. Si basa sull’equazione integral del flusso del campo elettrico:
ʃE * dA = Q/εo
dove:- E è il campo elettrico 🔌
- dA è il vettore area elementare sulla superficie chiusa (S) 📐
- Q è la carica totale racchiusa dalla superficie 🔋
Per esempio, per una sfera uniformemente carica di raggio (R) e carica totale (Q):
- All’interno della sfera (a distanza ( r < R ) dal centro): Grazie alla simmetria sferica, il campo elettrico dentro la sfera è: E = 1/4 πεo * Qr/R3*r
- All’esterno della sfera (a distanza ( r > R ) dal centro): Il campo elettrico è lo stesso come se tutta la carica fosse concentrata nel centro della sfera:E = 1/4 πεo * Qr/r2*r
Quando intendiamo studiare i campi elettrici è fondamentale conoscere la legge di Gauss.
Essa offre un metodo ben preciso per poter effettuare il calcolo del flusso di campo elettrico all’interno di una superficie chiusa.
Inoltre, questa legge fa parte dei teoremi più importanti appartenenti all’elettromagnetismo, insieme alle leggi di Maxwell e al teorema di Biot-Savart. La sua formulazione è da attribuire a Carl Friedrich Gauss e risale al XIX secolo.
Il teorema di Gauss per il campo elettrico: l’enunciato
Il teorema di Gauss è conosciuto anche come teorema della divergenza e serve a dimostrare che:
il flusso del campo elettrico tramite una superficie chiusa è direttamente proporzionale alla carica racchiusa all’interno della superficie divisa per la costante dielettrica del vuoto 🔌
Per capirlo meglio facciamo un veloce ripasso di due concetti determinanti:
- campo elettrico 🔋
- flusso del campo elettrico ⚡️
Quando parliamo di campo elettrico ci riferiamo a una grandezza fisica di tipo vettoriale relativa al campo che si forma attraverso una o più cariche elettriche facenti parte dello spazio.
In generale, si definisce campo di forze una regione di spazio in cui è attiva una determinata forza a distanza e la forza elettrica, come quella gravitazionale, è una forza a distanza che agisce fra corpi dotati di carica.
In assenza di contatto fra corpi l’azione della forza elettrica avviene mediante perturbazione dello spazio circostante. Il campo elettrico è la perturbazione dello spazio generata dalla presenza di una carica elettrica.
Il campo elettrico si rappresenta mediante le linee di forza che esprimono la direzione del campo generato da cariche elettriche poste in una determinata regione di spazio.
Le cariche positive generano linee con verso uscente, quelle negative con verso entrante. In un dipolo costituito da due cariche opposte le linee vanno dalla positiva alla negativa.
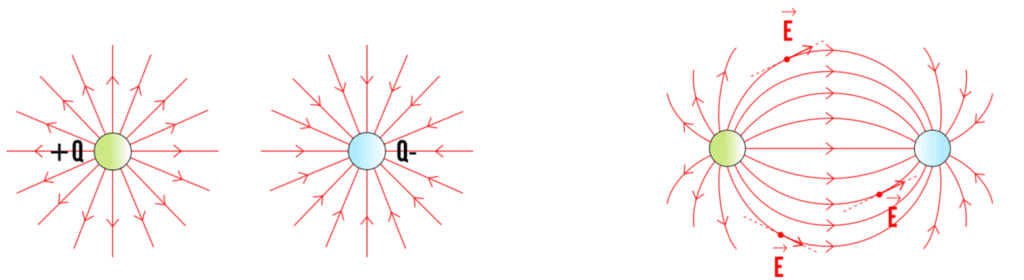
Invece il flusso del campo elettrico viene generato “dall’integrale del capo elettrico” sopra una data superficie. Esso è una grandezza pari al prodotto scalare fra il vettore di cui si vuole conoscere il flusso e la normale alla superficie.
Il teorema di Gauss trova molte applicazioni pratiche in elettrostatica e permette di trarre alcune importanti conclusioni:
- Nelle superfici chiuse (conduttori) le cariche elettriche si distribuiscono soltanto sulla superficie 🔌
- Il campo elettrico interno ad un conduttore è nullo ❌
- Tutti i punti di un conduttore, in condizioni di stasi delle cariche, hanno un valore uguale associato all’energia potenziale ⚡️
La formula del teorema di Gauss
La formula della legge di Gauss è data da
ϕ = Q ⁄ εo
dove:
- ϕ è il flusso racchiuso dalla superficie 🔌
- Q è la carica totale all’interno di una data superficie ⚡️
- εo rappresenta la costante elettrostatica 📚
Con il teorema di Gauss, quindi, vengono collegati in termini semplici il flusso delle linee del campo elettrico alle cariche contenute all’interno della superficie racchiusa.
La formula che esprime tale concetto è
ϕ = E.dA = q netto ⁄ εo
Il flusso elettrico netto equivale a 0 se la superficie non contiene cariche. Il numero di linee di campo elettrico che, invece, entra all’interno della superficie è uguale a quello di linee di campo che escono dalla superficie.
Per poter comprendere meglio tale concetto, è bene che tu sappia che il flusso elettrico non è influenzato da altre cariche esterne alla superficie stessa. In più, sono le altre cariche elettriche che possono fungere da sorgenti o da assorbitori di campo elettrico.
A tal proposito, è fondamentale notare come la variazione del campo magnetico non può agire come sorgente o pozzo di campo elettrico.

Considerando che racchiude una carica netta, il flusso netto per la superficie a sinistra è differente da 0. Dato che la superficie di destra non ha al suo interno alcuna carica, il flusso netto equivale a 0.
Ecco perché spesso viene indicato che il teorema di Gauss, in realtà, rappresenta una ripetizione della legge di Coulomb, che si ottiene in modo semplice applicandolo a una carica puntiforme circondata da una sfera. Questo evidenzia ancor di più come il teorema di Gauss e la legge di Coulomb siano strettamente correlate.
Dimostrazione del teorema di Gauss
Consideriamo una carica puntiforme (Q) al centro di una sfera di raggio (r). Per la simmetria sferica, il campo elettrico (E) generato dalla carica è uniforme sulla superficie della sfera e diretto radialmente verso l’esterno o l’interno a seconda del segno di (Q).
Per la legge di Coulomb, il campo elettrico (E) a distanza (r) da una carica puntiforme è: E = Q/4 πεor2
Il flusso ϕ attraverso la superficie sferica è dato da: ϕ = ʃE * dA = E * 4πr2
L’integrazione di E * dA su tutta la superficie sferica copre tutta l’area senza alcuna componente angolare ⚡️
Questa dimostrazione si basa sulla simmetria sferica e sulla distribuzione uniforme del campo elettrico. Se la distribuzione di carica o la geometria sono più complesse, si usano metodi più avanzati, ma il principio di base rimane lo stesso.
Per la legge di Gauss il flusso del campo elettrico attraverso una superficie è sempre proporzionale alla carica totale racchiusa, indipendentemente dalla forma della superficie.
La chiave sta nell’applicare correttamente il concetto di flusso e capire come il campo elettrico si distribuisce in relazione alla geometria della superficie chiusa e alla distribuzione delle cariche interne.
Applicazioni del teorema di Gauss
Applicando il teorema di Gauss per diverse condizioni si ottengono varie formule.
Ad esempio:
- in un mezzo con una costante dielettrica K, l’intensità del campo elettrico vicino a un conduttore piano carico ha la seguente formula: E = σ ⁄ K εo ⚡️
- L’intensità del campo elettrico vicino a un foglio piano di carica, invece, è E = σ ⁄ 2K εo, dove σ è la densità di carica superficiale ✍️
- Quando il mezzo dielettrico è l’aria, la formula diventa: Earia = σ ⁄ εo 💨
- In un condensatore, il campo tra due piastre parallele è E = σ ⁄ εo, dove σ è indica la densità di carica superficiale 🔌
- Nel caso di una distanza di ‘r’ per una linea di carica infinita, la formula da applicare è: E = (1⁄4 n * π r ε0) (2π ⁄ r) = λ ⁄ 2π r εo, dove λ rappresenta la densità di carica lineare 📏
Gabbia di Faraday
Forse avrai sentito parlare della gabbia di Faraday, strumento che consente di sfruttare quanto appena visto nel teorema di Gauss. Sebbene possa sembrare qualcosa di insolito, questa gabbia è molto comune e protegge tutti noi in tantissimi casi di pericolo potenziale.
Il nome di tale sistema deriva dal suo inventore, il fisico Michael Faraday, il quale decise di creare questo involucro metallico che, quando caricato, consente alle diverse cariche di distribuirsi sulla parte esterna senza farle entrare all’interno della gabbia. Il campo elettrico della parte interna, dunque, rimane nullo.
Ma perché il teorema di Gauss e questo fenomeno sono legati? In poche parole, il fatto che la gabbia funzioni è una conseguenza del teorema stesso.
Prova a pensarci: se il flusso del campo elettrico è strettamente connesso alla carica contenuta all’interno della superficie considerata, non c’è alcuna possibilità che si crei un campo elettrico che, in precedenza, non era presente.
Per farti un esempio che ti chiarisca il concetto, possiamo considerare come gabbia di Faraday la rete di metallo che scherma i forni a microonde, il telaio di una macchina o la fusoliera di un aereo, strumenti che ci proteggono in caso di fulmini.
Ripassa glia argomenti di fisica per il test di ammissione
Bene! Siamo alla fine di questo episodio, spero ti sia stato utile per ripassare il teorema di Gauss e le formule per calcolare il campo elettrico 🧠
Non dimenticare che se cerchi supporto e se ti stai preparando per il test di ammissione all’università, puoi contare su Futura e sulla preparazione ADT 🚀
Con Futura hai tutto il materiale per la teoria insieme a uno strumento potente e versatile per prepararti al meglio con:
- simulazioni illimitate per cimentarti in esercitazioni personalizzate che si adattano ai tuoi progressi 💯
- archivio per monitorare i tuoi progressi e scoprire quali argomenti necessitano di ulteriore approfondimento 📚
- ALICE, il tutor virtuale di Accademia Dei Test, per ottenere spiegazioni personalizzate e suggerimenti mirati 🤖
Con Futura, hai la possibilità di esercitarti sui quiz ministeriali, ottimizzare il tuo tempo e massimizzare i tuoi sforzi.
Preparati con ADT, scopri l’offerta più adatta a te 🚀
Inoltre, se vuoi confrontarti (o avere conforto) non esitare ad unirti alla nostra community Telegram composta da studenti con cui potrai condividere gioie e dolori della preparazione al test 🥵
Ti aspettiamo, alla prossima 🚀







