Ciao Doctorz, in questo episodio facciamo la conoscenza del moto armonico e delle sue formule.
Il moto armonico è l’ultimo membro della famiglia della fisica cinematica, diciamo che è il cugino del moto circolare.
Sai perché un pendolo oscilla avanti e indietro con un ritmo così costante? Oppure perché le molle ritornano sempre alla loro posizione di riposo dopo essere state stirate o compresse?
Probabilmente no e ci sta, siamo qui per questo.
In ogni caso, le risposte risiedono nei fenomeni fisici descritti dal moto armonico e dalle sue formule.
I corsi ADT ti offrono:
- simulazioni illimitate con oltre 36.000 quiz ministeriali e tantissime modalità di esercitazione sulla nostra piattaforma Futura 💯
- chat diretta con il tuo tutor personale per ottenere supporto anche dopo l’orario di lezione 📚
- materiale di studio completo 📖
- lezioni in diretta e on demand con docenti qualificati ed esperti nella preparazione ai test 🧠
Che ti piaccia o no, il moto armonico è ovunque intorno a noi: dal movimento delle onde del mare al battito del cuore, fino ai compiti in classe e ai TOLC 🥶.
Ma cosa significa esattamente e come possiamo descriverlo matematicamente?
Nei prossimi scroll, ci immergeremo nel mondo del moto armonico e delle sue formule.
Non preoccuparti se la matematica non è il tuo forte, con me sei in buona compagnia (🥲), ma farò del mio meglio per rendere tutto il più comprensibile possibile.
Quindi iniziamo e facciamo un po’ di chiarezza!
Cos’è il moto armonico e cosa vogliono dire le formule
Iniziamo dalle basi e diamo una definizione.
Il moto armonico descrive un movimento oscillatorio che segue un ritmo ben preciso.
Un oggetto in moto armonico oscillerà avanti e indietro attorno a un punto di equilibrio in un modo molto particolare, seguendo una traiettoria descritta da una funzione seno o coseno.
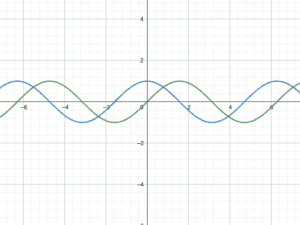
Questo significa che se tracci la posizione dell’oggetto nel tempo, otterrai un bel grafico sinusoidale. Fantastico, no? No, però qualcuno dovrà pur farlo (e purtroppo quel qualcuno sei tu).

Per un grafico, però, abbiamo bisogno di formule ed equazioni, che ci permettano di rappresentare questo tipo di spostamento.
Vediamo quindi il moto armonico e le sue formule.
Nello specifico ne consideriamo tre, che permettono di calcolare la posizione, la velocità e l’accelerazione di un oggetto in moto armonico in qualsiasi momento.
- Legge oraria del moto armonico.
La formula descrive la posizione di un oggetto in moto armonico in un dato momento.
È data da: x(t) = A cos(ωt + φ).
- Velocità nel moto armonico.
La velocità di un oggetto in moto armonico varia nel tempo.
La formula per la velocità è: v(t) = -ωA sin(ωt + φ).
- Accelerazione nel moto armonico.
L’accelerazione in un moto armonico è sempre diretta verso il punto di equilibrio.
La formula per l’accelerazione è data da: a(t) = -ω²A cos(ωt + φ).
La legge oraria
Ripartiamo dalla legge oraria del moto armonico e capiamo cosa esprimono le variabili contenute nella sua formula.
Quest’ultima è espressa dalla funzione: x(t) = A cos(ωt + φ).
Dove:
- x(t) è la posizione dell’oggetto al tempo t;
- A è l’ampiezza del moto (la distanza massima dall’equilibrio);
- ω è la velocità angolare (2π diviso il periodo del moto);
- t è il tempo;
- φ è la fase iniziale (la posizione dell’oggetto al tempo t = 0).
Facciamo due piccole precisazioni.
La frequenza è il numero di oscillazioni che un oggetto esegue in un secondo ed è legata alla velocità angolare ω attraverso la formula ω = 2πf.
Si misura in Hertz (Hz) ed è l’inverso del periodo (lo vediamo subito qui sotto, don’t panic 😉).
Quindi, una frequenza più alta significa più oscillazioni in un dato lasso di tempo.
La velocità nel moto armonico
Per quanto riguarda le altre due formule viste poco più su (velocità e accelerazione) possiamo dire che la velocità è:
- massima quando l’oggetto passa attraverso il punto di equilibrio;
- minima (cioè zero) quando l’oggetto raggiunge i punti estremi del suo moto.
Il tempo necessario per un’oscillazione completa è dato dal periodo.
Quest’ultimo è dato dalla durata di un singolo ciclo di moto e si misura in secondi (s).
Nel contesto del moto armonico, il periodo è l’inverso della frequenza (T = 1/f) e può essere collegato alla velocità angolare tramite la formula ω = 2π/T.
Quando il valore del periodo è elevato vuol dire che l’oggetto in spostamento con moto armonico impiega più tempo per completare un ciclo.

L’accelerazione nel moto armonico
Al contrario della velocità, l’accelerazione è:
- massima nei punti estremi del moto;
- minima (cioè zero) quando l’oggetto passa attraverso il punto di equilibrio.
Questo ci permette di capire il motivo per cui l’oggetto rallenta o accelera in base alla distanza dal punto di equilibrio.
Per comprendere questa differenza tra velocità e accelerazione, possiamo farci aiutare dall’analisi del moto del pendolo.
Infatti, un pendolo che oscilla avanti e indietro è un esempio di moto armonico.
Questo perché la velocità del pendolo cambia durante l’oscillazione. Infatti, è massima quando passa per il punto di equilibrio e minima (zero) ai punti estremi dell’oscillazione.
L’accelerazione, invece, è sempre diretta verso il punto di equilibrio, cioè il pendolo è sempre “spinto” verso il centro.
Capire le formule: esempi ed esercizi
Per capire meglio tutte le formule e i concetti che abbiamo appena visto approfondiamo proprio il movimento del pendolo.
L’ampiezza di un pendolo, A, sarebbe la massima distanza che il pendolo si allontana dal centro durante l’oscillazione.
La fase iniziale, φ, è la posizione iniziale del pendolo.
Il periodo del pendolo, T, sarebbe il tempo che impiega per fare un’oscillazione completa avanti e indietro.
La frequenza, f, sarebbe l’inverso del periodo e rappresenta il numero di oscillazioni che il pendolo fa in un secondo.
Infine, la velocità angolare, ω, è 2π/T o 2πf, e rappresenta la velocità con cui il pendolo oscilla.

Vediamo meglio questi concetti sul moto armonico e le sue formule con un esercizio con risposta multipla.
Un pendolo ha un periodo di oscillazione di 1s. Se si quadruplica la lunghezza del pendolo, che valore assumerà il periodo?
Le alternative di risposta sono:
- A. 0,1 s;
- B. 0,25 s;
- C. 4s;
- D. 2s.
Per risolvere questo problema, dobbiamo usare la formula del periodo di un pendolo semplice, che è:
T = 2π √(L/g).
In questo caso, sappiamo che il periodo iniziale del pendolo è 1s.
Vogliamo sapere quale sarà il nuovo periodo se la lunghezza del pendolo viene quadruplicata.
Se chiamiamo T1 il periodo iniziale e L1 la lunghezza iniziale, e T2 il nuovo periodo e L2 la nuova lunghezza, allora abbiamo:
- T1 = 2π √(L1/g);
- T2 = 2π √(L2/g).
Ma poiché L2 = 4L1 (perché la lunghezza del pendolo è quadruplicata), possiamo scrivere:
- T2 = 2π √(4L1/g).
È possibile semplificare questa espressione estrarre la radice quadrata del 4, ottenendo:
- T2 = 2 * 2π √(L1/g).
Questo ci dice che il nuovo periodo è due volte il periodo iniziale.
Quindi, se il periodo iniziale era 1s, il nuovo periodo sarà 2s.

Per questo episodio è tutto, spero ti sia stato utile per ripassare i concetti principali sul moto armonico e le sue formule.
Se vuoi una spiegazione più approfondita puoi dare un’occhiata al nostro ripasso della cinematica su YouTube, completo di teoria ed esercizi per ripetere i punti salienti dei tipi di moto in fisica.
Inoltre, non dimenticare che se cerchi un sostegno più strutturato e personalizzato abbiamo ciò che fa per te: i corsi di preparazione di ADT!
I nostri corsi ti offrono tutto ciò di cui hanno bisogno per ottimizzare al meglio la preparazione.
Infatti, ti offrono lezioni (live e on demand) insieme al simulatore con più di 30000 quiz ministeriali che puoi personalizzare per migliorare i tuoi punteggi giorno dopo giorno.
Scopri di più qui sul sito oppure scrivici ( su WhatsApp, Telegram o Instagram) per ottenere tutte le informazioni sulla preparazione per i TOLC di luglio (e non solo)!
Ciao Doctorz, ci vediamo presto, alla prossima! 🧡🚀





